Abstract Data Types, Algebraic Data Types and Algebraic [Data] Structures
Second draft alert!Discussing the differences between abstract data types, algebraic data types, and algebraic [data] structures.
I wasn't intending to write this article but then @chvest asked me to clarify (see below), so hopefully this will be a short, sweet, and informal explanation that does the job.
@susanpotter I thought those were the same thing. What’s the difference?
— Chris Vest (@chvest) November 27, 2012
To be able to articulate the difference between the two above, I first want to review the notion of an abstract data type often abbreviated as ADT simply because some developers may confuse ADTs and algebraic data types (AlgDT).
Going back to basics...
Abstract Data Type (ADT)
This refers to a specification of a data type like a stack or queue where the specification does not contain any implementation details at all, only the operations for that data type. This can be thought of as the contract of the data type.
In computer science the most common example of this is a stack. The stack ADT specifies three operations for the type, which informally looks like:
- push - which allows an element to be pushed on the top of the stack
- pop - which allows an element to be popped off the top of the stack
- peek - which allows the top element to be inspected without taking it off the top
We can find implementations of many commom ADTs across many lanaguages and sometimes multiple implementations of the same ADT in the same langauge or standard library for a language or runtime. Thus why the specification is an abstract data type as it doesn't dictate implementation details. :)
A better specification would list inputs, outputs, and expected effects more formally, but since this should be a pretty familiar notion to most practicing developers today, I will not dwell on it.
Algebraic Data Type (AlgDT)
An algebraic data type can take many forms:
- Sum type
- Product type
- Unit type
- Recursive type
- Hybrid type
I will only discuss sum and product types here.
Sum Types (aka Tagged Unions)
The notion of a type having a known, and exhaustive list of constructors where the type must be constructed by exactly one of these is known as a Tagged Union. I have also seen it called a sum type. In fact, I much prefer the latter so expect me to use that form in this and later articles.
A sum type is a concrete type definition where our type is one of N known constructions, where N is a finite positive integer. Each construction may hold zero or more components of specific types (although these components may vary from construction to construction.
Practically speaking N should be reasonably small most of the time (in the single or double digits) simply because all good software developers are lazy and dislike boilerplate code! :)
Let's step back to a basic example of a sum type (which is one variety of AlgDTs) to illustrate the difference between a sum type and a pure product type.
// Scala here to mix it up :)
sealed trait USCoin { def value: Int }
case object Penny extends USCoin { def value = 1 }
case object Nickel extends USCoin { def value = 5 }
case object Dime extends USCoin { def value = 10 }
case object Quarter extends USCoin { def value = 25 }
case object Dollar extends USCoin { def value = 100 }
The above just tells Scala that there is this trait (in this case we can
pretend it is the same as the LHS of Haskell's data declaration, but it
isn't always this way), USCoin, that has a finite, and known
number of constructors up front (typically how case classes in Scala get used
[well]). Note that the trait is sealed. For non-Scala people
this just means that outside of this source file, no extensions of this
trait are allowed. i.e. the compiler can guarantee that consumers of our
libraries, or toolkits cannot extend USCoin. In this particular scenario
that is probably what we want (not allowing consumers of our code to
extend this). The likelihood that the US central bank would introduce
new coins or take existing coins out of circulation before we update our
library in time to cater for it, is pretty unlikely. However, there is
another good reason why we might want this too: we can know we have
exhaustively catered for all constructions of USCoin in our supporting
logic or calculations.
You might be wondering how this can be done. Let us try to use this code
(coming to a GitHub repository near you soon) to explore this idea
further. So fire up sbt console in the algdt
subproject in the git repository.
scala> import funalgebra.algdt._
import funalgebra.algdt._
scala> object VendingMachine {
| def accepts(coin: USCoin): Boolean = coin match {
| case Penny => false
| case Nickel => false
| case Dime => true
| case Quarter => true
| }
| }
:12: warning: match is not exhaustive!
missing combination Dollar
def accepts(coin: USCoin): Boolean = coin match {
^
defined module VendingMachine
What happened here is that we forgot to match on the Dollar
constructor for USCoin sum type and the Scala
compiler warned us about it. If you find you want this behaviour for
a particular data type definition, then you probably want to define it
as a sum type this way.
Product Types (aka Record Types)
In the language of abstract algebra, which computer scientists in programming language theory appear to have adopted, a data type with exactly one constructor is isomorphic to what is often called a product type that takes an ordered list of typed operands. Informally these are sometimes called Record Types.
@chvest pointed out while reviewing this article that the archetypal product type is the tuple. For example, perhaps we want to represent an image element in a HTML page. We might initially represent it as the following tuple:
(String, Int, Int)
Here we take a string (the source URL), an integer (the width), and a second integer (the height). The problem with tuples is that this might also represent any number of issues. It is hard to know what it is referring to. Enter product types.
In Scala below we can represent an image element in HTML as the following case class.
case class ImageElement(sourceUrl: String, width: Int, height: Int)
Since pure product types only have one constructor for a type, we can
eliminate the trait or abstract class type definition that
we used in the sum type example above with USCoin.
Sum-Product Type Hybrids

How about a social network event notification. Let's take Facebook. Whenever you sign into Facebook (or whatever social network you might use), you will likely be greeted with a visual indication of any notifications you might have since you last signed in. Things like friends liking your statuses, comments, or making comments on your posts or posts you have commented on yourself.
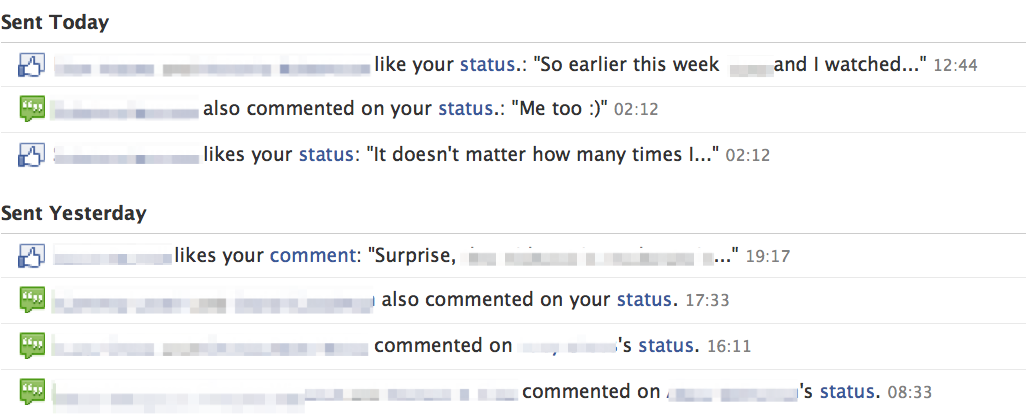
So a first stab at modeling this with an algebraic data type in Haskell might look like:
import Data.DateTime
-- Assumes User is defined elsewhere and imported
-- Assume Status and Comment types are already defined
data Notification = CommentNotification Status [User] DateTime
| CommentLikeNotification Comment [User] DateTime
| PostLikeNotification Status [User] DateTime
What did I actually do? Well if we look at the different notifications we see there are a variety of constructions of notification events, including:
- When one of your statuses is liked it tells you who and at what time last action was taken
- When one of your comments is liked it tells you who and the time last action was taken
- When a post you commented on is commented on it tells you who and the time last action was taken
- ...
Let us dissect the Haskell code a little. The identifier on the LHS,
Notification, is the type. Then the RHS contains an
exhaustive list of possible constructors such as:
CommentNotification, CommentLikeNotification,
PostLikeNotification for our simple model.
Now we could have modeled Notification data type a little
differently. Let us consider the following modeling of the domain:
import Data.DateTime -- Assumes User is defined elsewhere and imported -- We might want to add more constructors for Post sum type of a more -- complete model of Facebook notifications, but left as a homework to -- reader, because every algebra lesson has this ;) data Post = Status Text DateTime | Comment Text DateTime data Notification = Notification Post [User] DateTime
This model of the domain of Facebook notifications uses a pure
product type for the Notification type definition
and a hybrid sum-product type for the Post type.
Exactly how you model this domain will depend on what properties you would like the various types to possess. In fact, there are many ways you can model this domain with various forms of algebraic data types (AlgDT). It all depends on your program's view of the domain.
There is no one presice view of a particular domain, it depends on your program's functionality. For example, if you are building a front office trade posting system, you are unlikely to need to model the historical view of a security or instrument type. You just need to know the active identifier (e.g. ticker, ISIN, CUSIP, internal id, etc.) for the security being traded today to flow through correctly.
However, a knowledge management tool may need to model a security or instrument to have a historical view (e.g. how a corporate action impacted a security in the past, or the historical view of identifications or vendor symbols).
Algebraic [Data] Structures
Algebraic [data] structures on the other hand may not be data types specifically, but they might be. An algebraic structure embodies a structure with consistent and known algebraic properties. In my recent SCNA talk, I described monoids specifically, which has a specific structure and properties that must be conformed to (or it isn't really a monoid at all).
In fact, in Haskell a Monoid is defined as a typeclass, which
is not an AlgDT in the above
definition, however, you can view the type class declaration as an
ADT by the above definition as the
it specifies only an interface and contract without describing
implementation details. The instance definitions of Monoid
for specific types will contain the implementation details.
Conclusion
It isn't necessarily the case that an algebraic structure is also an ADT and it is possible that you could describe an algebraic structure as an AlgDT if/when it makes sense. Going forward in the Functional Algebra article series I will use the above definitions for these terms unless otherwise noted.